B3.7: Topologically Protected Circuits for Metrology
Subproject Leader: Alexander Shnirman
Institut für Theorie der Kondensierten Materie, KIT
Contributing Scientists:
Present: Ingo Kamleitner, Nicolas Vogt
Past: Martin Greiter, Holger Schmidt, Michael Schütt, Stephan Rachel,
In the last decade great progress has been achieved in observation and utilization of quantum phenomena in Josephson junction circuits. Macroscopic quantum effects have been realized based on the coherent properties of superconductors. At present the main activities in this field are focused on optimizing qubit circuits and on the realization of a quantum information processor. Here we focus on a different subject. We study the possibility of using collective excitations in arrays of Josephson elements for metrological applications with high level of precision. We conduct research into the following three subjects:
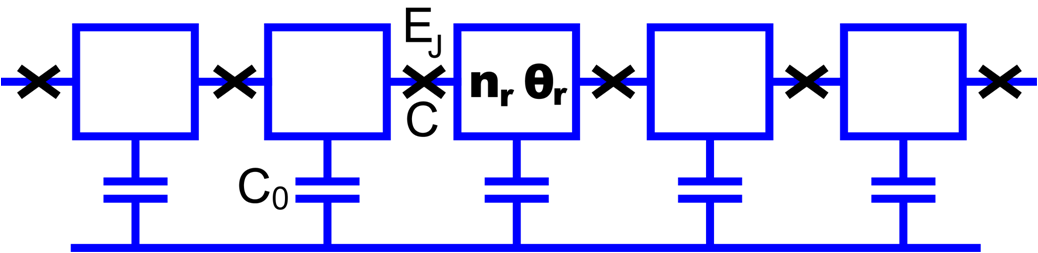
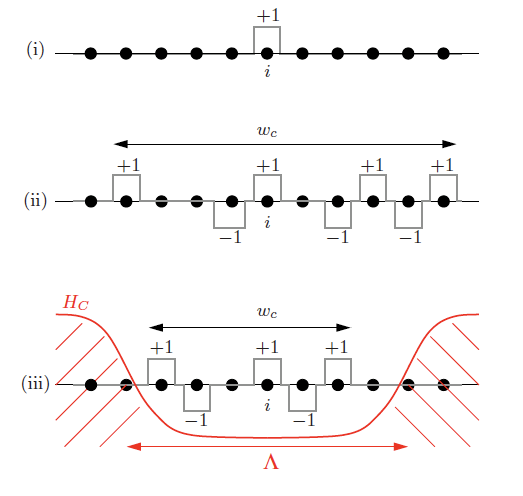
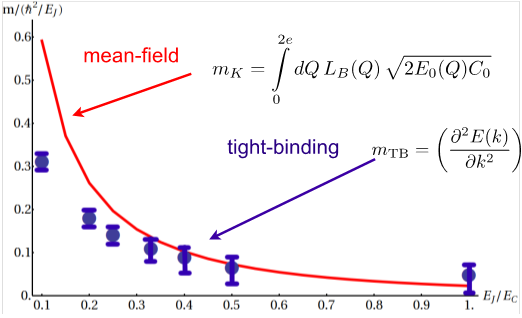
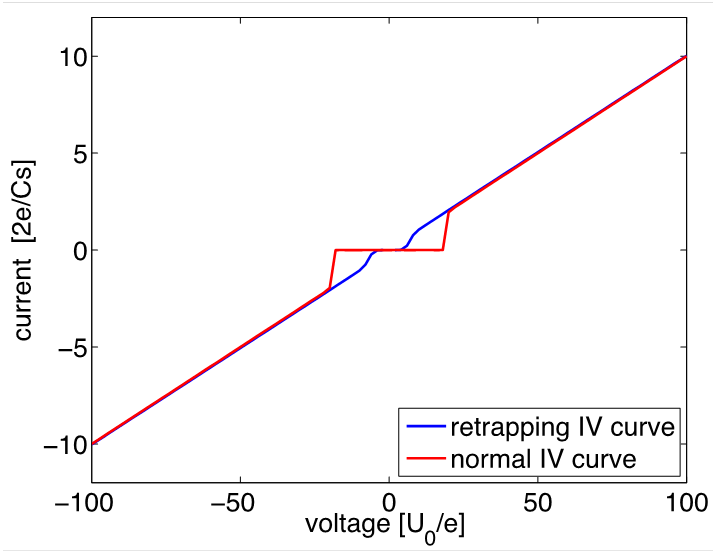
- Charge transport in gated arrays of Josephson junctions. We are motivated by the experiments [1,2] in which Cooper pair transport was investigated in long arrays of dc-SQUIDs. Depending on the external magnetic field, which controls the effective Josephson energy, either an insulating or (quasi) superconducting behavior is observed. Thus far we have theoretically studied the propagation of charge solitons in clean infinite arrays. Using the many body tight binding approach we have determined the dispersion relation of a charge soliton considering the dressing of cooper pairs in the array by the formation of dipoles [3,4]. A quadratic dependence of the kinetic mass of a soliton on the Josephson coupling energy is found, giving a possible explanation for the quadratic dependence of the conductivity on the Josephson energy found in experiments. In the mean field approach [4] we succeeded to derive a sine-Gordon-like equation of motion governing the soliton dynamics in the adiabatic limit. Applied to a finite Josephson junction array the mean field theory yields the Frenkel-Kontorova model, the discrete analogue to the sine-Gordon model. Accounting for dissipation due to Landau-Zener transitions numerical simulations produce hysteretic I-V-curves as they are found in experiments.
- Topological and geometric pumping. A Cooper pair pump is a superconducting device, consisting of one or more islands, which are coupled to two leads via Josephson junctions or SQUIDs. Cooper pairs can be pumped through the devise by cyclic modulation of the Josephson couplings and / or the electrostatic potential of the islands. We investigate the influence of noise on the Cooper pair pumping. While zero temperature noise has no influence on adiabatic ground state pumping (it even stabilizes adiabaticity), finite temperature noise can excite the system and therefore can change the transferred charge per pumping cycle. We have developed [5] a master equation technique in the Floquet basis, which allowed us analyzing pumping in various regimes. An intriguing possibility is to make pumping topologically exact [6].
- Two-dimensional Josephson arrays with topological excitations. In the context of quantum computations several kinds of Josephson arrays were proposed (see, e.g., [7]) to realize models with topological protection of the degenerate ground state and with anionic excitations. First experimental confirmation appeared recently [8]. It is well known, e.g. from the theory of the quantum Hall effect, that in materials with non-trivial topology a single charge can be pumped to or from the edge of the sample by adiabatic insertion of a flux quantum, e.g., into a hole in the sample (Laughlin’s argument). This quantization of the pumped charge is extremely robust against disorder. We investigate similar properties in the topological Josephson arrays. If found, such a phenomenon would be very attractive for metrological applications.
References
| [1] | D. B. Haviland and P. Delsing, Cooper pair charge solitons: The electrodynamics of localized charge in a superconductor, Phys. Rev. B 54, R6857 (1996) |
| [2] | R. Schäfer, H. Rotzinger, A. Ustinov (private communication) |
| [3] | S. Rachel and A. Shnirman, Theory of small charge solitons in one-dimensional arrays of Josephson junctions. Phys. Rev. B 80, 180508(R) (2009) |
| [4] | J. Homfeld, I. Protopopov, S. Rachel, and A. Shnirman, Charge Solitons and their dynamical mass in one-dimensional arrays of Josephson Junctions. Phys. Rev. B 83, 064517 (2011) |
| [5] | I. Kamleitner, A. Shnirman, A time dependent Markovian master equation for adiabatic systems and its application to the Cooper pair pumping, arXiv:1108.3216 |
| [6] | R. Leone and L. Lévy, Topological quantization by controlled paths: application to Cooper pairs pumps, Phys. Rev. B 77, 064524 (2008) |
| [7] | B. Doucot, M.V. Feigelman, and L.B. Ioffe, Topological order in the insulating Josephson junction arrays, Phys. Rev. Lett. 90, 107003 (2003) |
| [8] | S. Gladchenko, D. Olaya, E. Dupont-Ferrier, B. Doucot, L.B. Ioffe, M.E. Gershenson, Superconducting Nanocircuits for Topologically Protected Qubits, Nature Physics 5, 48 - 53 (2009) |
List of Publications 2006-2011 as PDF
Subproject Report 2006-2010 as PDF