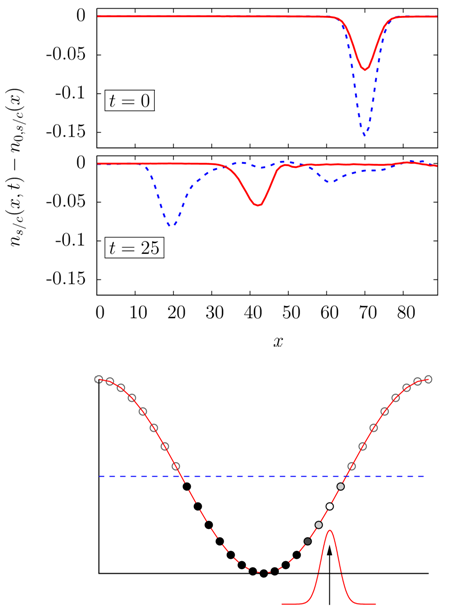
In one dimension interaction drive electronic systems into a state known as a Luttinger liquid. In this state the elementary excitations are of bosonic nature and spin and charge degrees of freedom decouple. Interestingly, their respective excitation velocities typically differ. The question that arises is whether this separation could be observable in a transport experiment. To this end we studied a model of 1D electrons, where an interaction region with a strong on-site repulsion is coupled to a non-interacting left and right lead. We then create a single, left moving hole excitation in the right lead and let it evolve. At the end of this scattering process of a single electronic excitation one may ask what we end up with. The main question that arises is, whether the outcome will be well defined spin-charge separated wave packets, or if a hole will be reconstructed, since we took one electron out of the system, or if there will emerge an incoherent superposition of many excitations. By performing simulations within the framework of the time dependent density matrix renormalization group (td-DMRG) [1] we have been able to establish that the observation of spin-charge separation should indeed be possible in a transport experiment. [2]

Transport Properties from Time Dependent Simulations

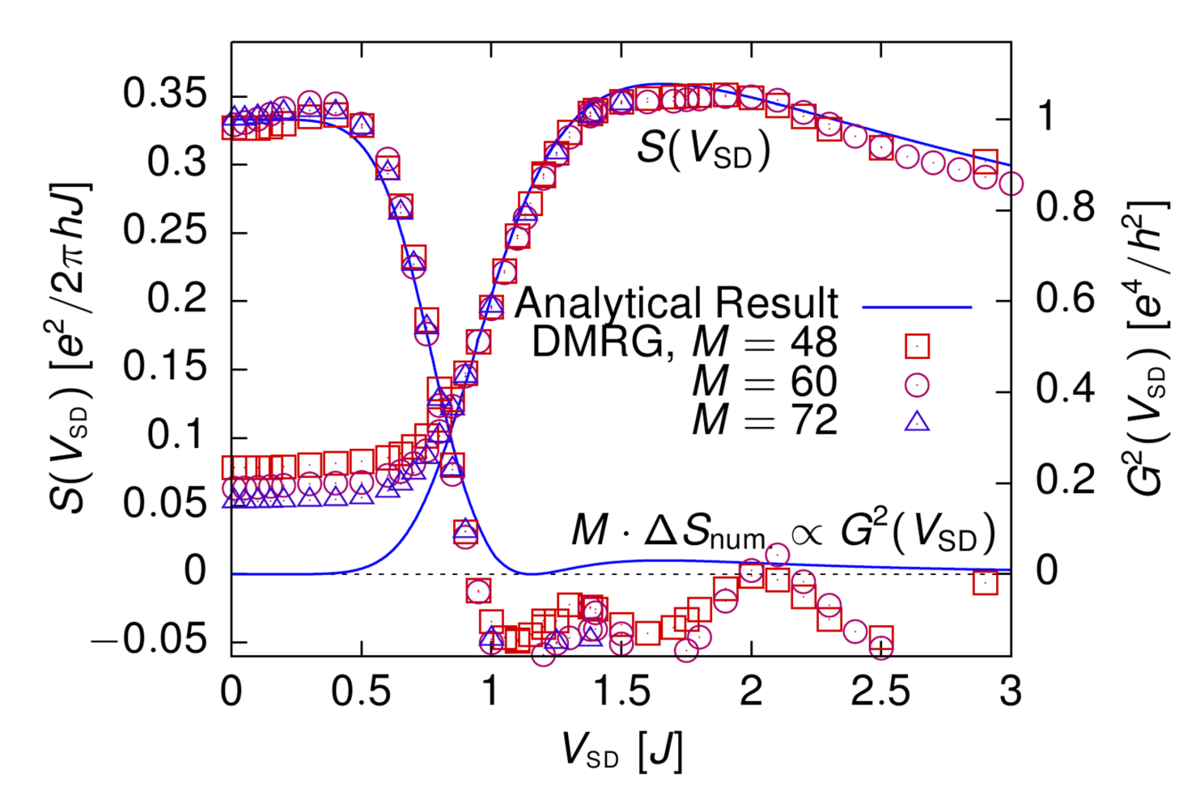
For interacting particles in small or low-dimensional structures where the screening of electrons is reduced, electron-electron correlations can have a strong impact on transport properties of nanostructures. In order to treat interaction and finite bias voltage rigorously and on equal footing we perform a complete simulation of a charge imbalance quench until we reach a quasi stationary regime, from which we can extract the corresponding current of the stationary state. By comparing our results to analytic calculations within the framework of the thermodynamic Bethe ansatz for the interacting resonant level model (IRLM) at its self dual point we find excellent agreement and a collapse of the numerical data on the universal analytic result for the I/V characteristic [3]. We then extended the method to obtain time dependent correlation functions. In [4] we studied shot noise, the zero frequency limit of the current-current correlation function. In contrast to the I/V characteristic shot noise is subject to strong finite size effects in the low voltage limit. Again we find excellent agreement between our numerical simulations and analytic calculations in the framework of the thermodynamic Bethe ansatz, where we could even establish that the finite size effects are proportional to G²/M, where G is the differential conductance and M is the number of sites in the leads. In our current work we are extending this approach to obtain the full counting statistic of the charge transport.

Exact Kohn-Sham Potentials for Density Functional Theory

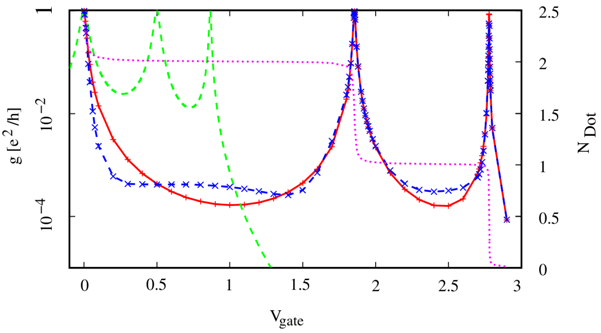
Within density functional theory (DFT) one describes electronic systems via an effective single particle description, the Kohn-Sham system, where the interaction effects are treated by  local potentials. The Hohenberg-Kohn theorem states that there exists a unique potential v(x) from which one obtains the exact ground state density and that this potential can be obtained by minimizing the energy functional corresponding to the system. However, this energy functional is not known in general and approximations have to be applied. We developed a reverse DFT procedure where we start from the local densities obtained within DMRG and determine numerically the potentials we need within the Kohn-Sham formalism to obtain the correct ground state densities. This enables us to study properties of the Kohn-Sham system itself not having to rely on approximative functionals. E.g., we could show that the linear conductance of a resonant chain is well described by the conductance of the corresponding Kohn-Sham particles provided that the exact potentials are used and the resonances are isolated [5]. 

References

List of Publications 2006-2011 as PDF

Subproject Report 2006-2010 as PDF