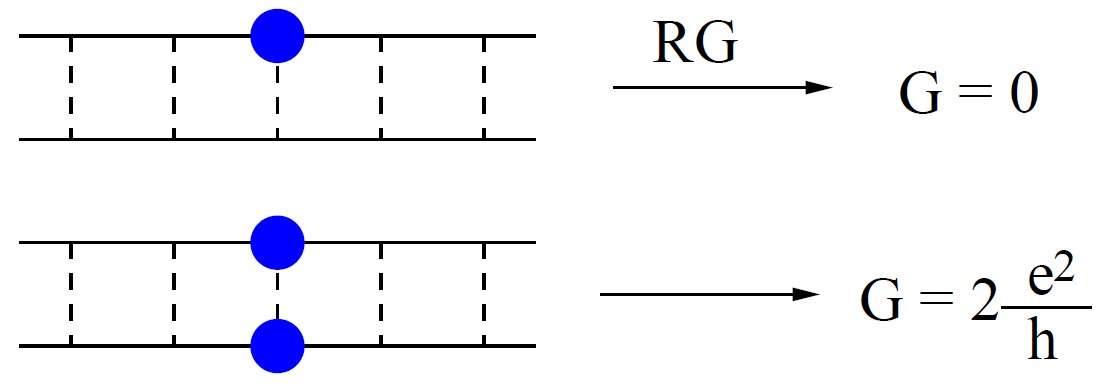B2.11: Correlation Effects and Disorder in Nanostructure Devices
Subproject Leader: Alexander Mirlin
Institut für Nanotechnologie, KIT
Contributing Scientists:
Present: Stephane Ngo Dinh
Past: Dmitri Gutman
Why are Correlations and Disorder Phenomena Important?
Electron interaction effects, as well as interference phenomena in disordered structures, become especially important when the system size and dimensionality is reduced. Thus, correlations and disorder phenomena play a prominent role in nanostructures, strongly affecting their electronic properties. This is, in particular, relevant to 1D and 2D nanostructures that serve as functional elements for present and future nanoelectronics.
Quantum Wires
Strongly correlated electron systems in 1D have become an area of immense interest from the perspective of both fundamental and technological aspects of nanophysics. In recent years, progress in nanofabrication technologies has made it possible to manufacture a variety of single- and few-channel quantum wires connected to the electric leads and to perform systematic transport measurements on the very narrow wires. The experimental realizations of quantum wires include, in particular, carbon nanotubes, semiconductor and metallic nanowires, and polymer nanofibers.
Central to the fascinating physics of 1D systems is that electron-electron interactions can have dramatic effects leading to the emergence of a strongly correlater state --- Luttinger liquid (LL). The latter constitutes a canonical example of a non-Fermi liquid, in which quasiparticle fermionic excitations are inappropriate to describe low-energy physics. At the foundation of the LL theory is the description in terms of bosonic excitations (plasmons, spinons). While the bosonization approach had facilitated significant progress in studying LLs, a number of most fundamental properties of these systems remained largely unexplored and have been investigated within this subproject. These include quantum interference, localization, and decoherence phenomena, effects induced by curvature of electron dispersion (e.g. Coulomb drag), and non-equilibrium physics.
Quantum Interference, Localization, and Decoherence
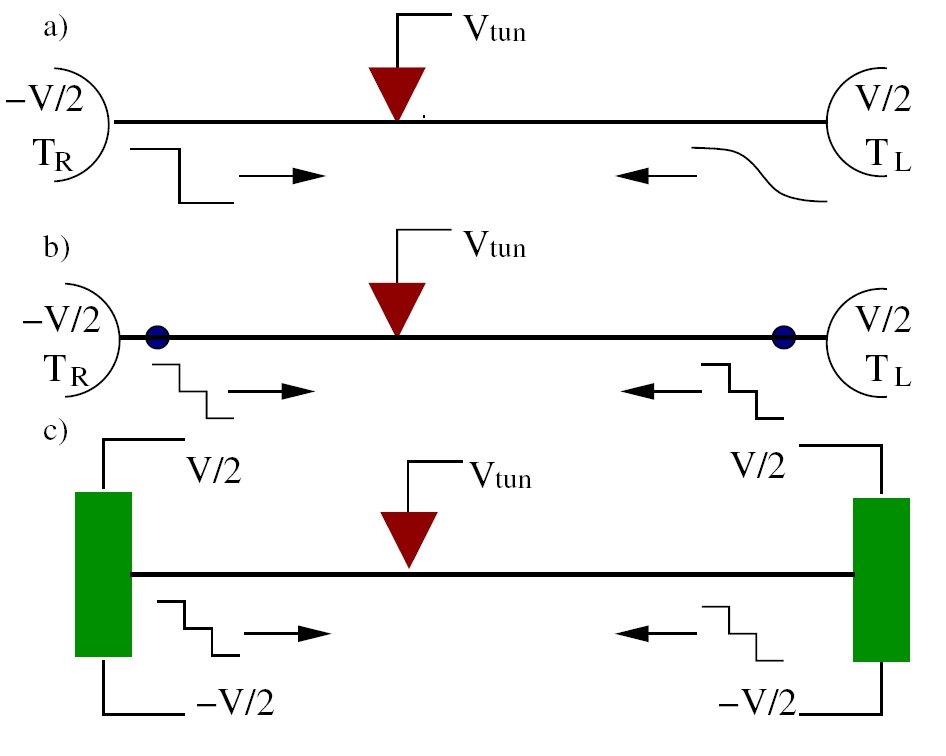
Quantum interference may dramatically alter transport in low-dimensional structures. In particular, coherent quantum scattering off disorder in a single-channel wire leads to exponential localization of all states at the scale of the mean free path. This is a manifestation of the famous Anderson localization, transforming a metallic wire into an insulator. In the presence of interactions and at finite temperature the non-equilibrium scattering processes lead to decoherence of electrons, reducing the effect of quantum interference. Understanding of interference and decoherence phenomena is of key importance for controlling transport properties of nanostructures.
Theoretical analysis of localization and decoherence of correlated electrons in a quantum wire is a highly non-trivial task, since the interference physics is naturally formulated in the fermionic (electronic) language, while low-energy excitations are bosons. We have solved this problem and developed a theory of disordered LL [1].
Non-Equilibrium Physics
Another challenge for us was the development of the theory of quantum wires under non-equilibrium conditions. The system can be brought out of equilibrium by application of a bias voltage. Recently developed experimental techniques permit to perform tunneling spectroscopy of nanostructures, giving access to the density of states and electron distribution function out of equilibrium. We have developed a novel framework of non-equilibrium bosonization that allowed us to explore these and related phenomena theoretically [2].
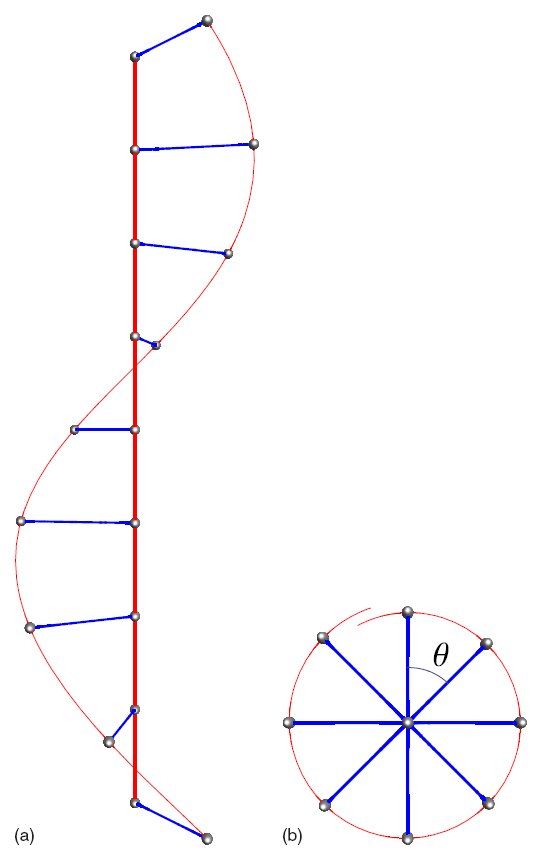
Quantum Ladders
The “ladder” systems are perhaps the simplest generalization of strictly one-dimensional chains. They consist of two chains (“legs”) which are connected by “rungs” providing hopping of electrons between the legs as well as their interaction. Experimental realizations of ladder systems were first discovered in copper oxides, and then in various organic materials. One should expect nano-fabricated samples with ladder geometry in foreseeable future. In this subproject we have explored transport and magnetic properties of the ladder structures [3,4].
2D Structures: Disorder, Interactions, and Quantum Phase Transitions
Disorder, electron-electron interaction, and their interplay induce a wealth of fascinating phenomena in 2D electronic structures. Our research in the field of 2D structures focused on investigation of disorder-induced quantum phase transitions (Anderson localization) and corresponding critical phenomena, as well as on the study of quantum effects of electron-electron interactions on transport properties of disordered 2D electron systems. In particular, we explored the multifractal nature of critical wave functions that is one of most remarkable properties of the Anderson metal-insulator transitions [5].
References
|
[1] |
I.V. Gornyi, A.D. Mirlin, and D.G. Polyakov, Phys. Rev. Lett. 95, 206603 (2005); Phys. Rev. B 75, 085421 (2007) |
|
[2] |
D.B. Gutman, Y. Gefen, and A.D. Mirlin. Phys. Rev. Lett. 101, 126802 (2008), Phys. Rev. B 80, 045106 (2009), Phys. Rev. B 81, 085436 (2010); S. Ngo Dinh, D.A. Bagrets, and A.D. Mirlin, Phys. Rev. B. 81, 081306 (2010) |
|
[3] |
C. Brunger et al, Phys. Rev. Lett. 100, 017202 (2008); D. N. Aristov et al., Phys. Rev. B 82, 174410 (2010) |
|
[4] |
S. T. Carr, B. N. Narozhny, and A. A. Nersesyan, Phys. Rev. Lett. 106, 126805 (2011) |
|
[5] |
F. Evers and A.D. Mirlin, Rev. Mod. Phys. 80, 1355 (2008) |
List of Publications 2006-2011 as PDF
Subproject Report 2006-2010 as PDF