B1.8: Electronic Properties of Graphene Nanostructures
Subproject Leader:
| Igor Gomyi | Institut für Nanotechnologie, KIT |
| Alexander Mirlin | Institut für Nanotechnologie, KIT |
Contributing Scientists:
Present: Sam Carr
Past: Dmitri Gutman
What is Graphene?
Graphene is a particularly intriguing two-dimensional structure with the quasi-relativistic dispersion law that has recently burst into the solid state physics. In 2004, researchers of Manchester University (UK) have succeeded to manufacture a monoatomic graphite layer – graphene – on an insulating substrate. This technological breakthrough has attracted a great deal of attention of leading experimental and theoretical groups over the world. In a very short time, a new area of research – the study of graphene-based structures – has emerged and become one of key research directions in the material science and condensed matter physics. The reason for this is exceptional properties of graphene that make this material highly interesting from the point of view of both fundamental physics and potential applications, most prominently, the carbon-based nanoelectronics. A.Geim and K. Novoselov were awarded the Nobel Prize 2010 for the discovery of graphene.
Why Graphene Differs from Others
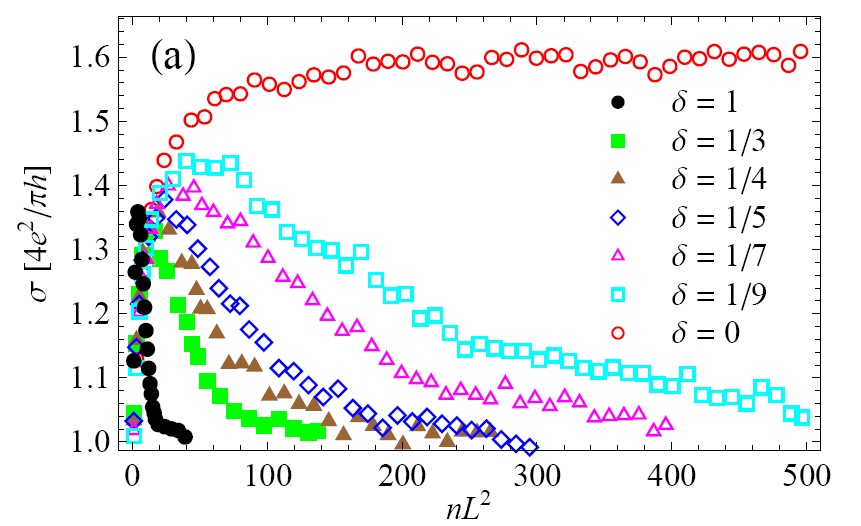
A hallmark of graphene is its unconventional electronic spectrum. Specifically, low-energy excitations in graphene are “relativistic” Dirac fermions with an effective “velocity of light” 106 cm/s. This leads to remarkable electronic properties of this material that have been revealed by transport measurements. In particular, graphene shows anomalous half-integer quantum Hall effect, which is observed up to room temperature, whereas it disappears at 30 K in the best semiconductor structures. This gives a clear signature of extremely robust, as compared to usual 2D systems, electron coherence in graphene. Very recent progress in purification of graphene and the novel technology of suspending graphene samples have lead to the experimental observation of fractional quantum Hall effect demonstrating the significant role of electron-electron interaction in graphene. Another remarkable discovery is that the conductivity of the undoped graphene in a broad temperature range (from 300 K down to 30 mK) is essentially independent of temperature and has a value close to 4e2/h . This discovery has attracted a great interest due to its apparent contradiction to the well-established theory of Anderson localization. This problem has been extensively studied within the Subproject.
Why Graphene is Important
The Dirac nature of carriers in graphene makes this material a unique “laboratory” for observation of such relativistic phenomena – normally expected in the high-energy physics – as Zitterbewegung and Klein tunneling, atomic collapse and vacuum polarization by a charged particle. The extraordinary electronic, thermal, and mechanical properties of graphene allow various applications, most prominently, the carbon-based nanoelectronics. Further prospective applications include devices for quantum information processing, composite materials, and sensors for individual molecules. Recently, a technology was developed that allows to synthesize graphene samples of macroscopic size (> 1cm) and to transfer them to various substrates. For applications, it is also very important that the electron concentration in graphene can be varied by applying a gate voltage, so that graphene can be used to realize a field-effect transistor. Further, a gap can be engineered and tuned in graphene-based structures. It appears to be possible to realize a room-temperature single-electron transistor on the basis of graphene. These findings open a way for developments of novel graphene-based electronics.
Developing Transport Theory in Graphene…
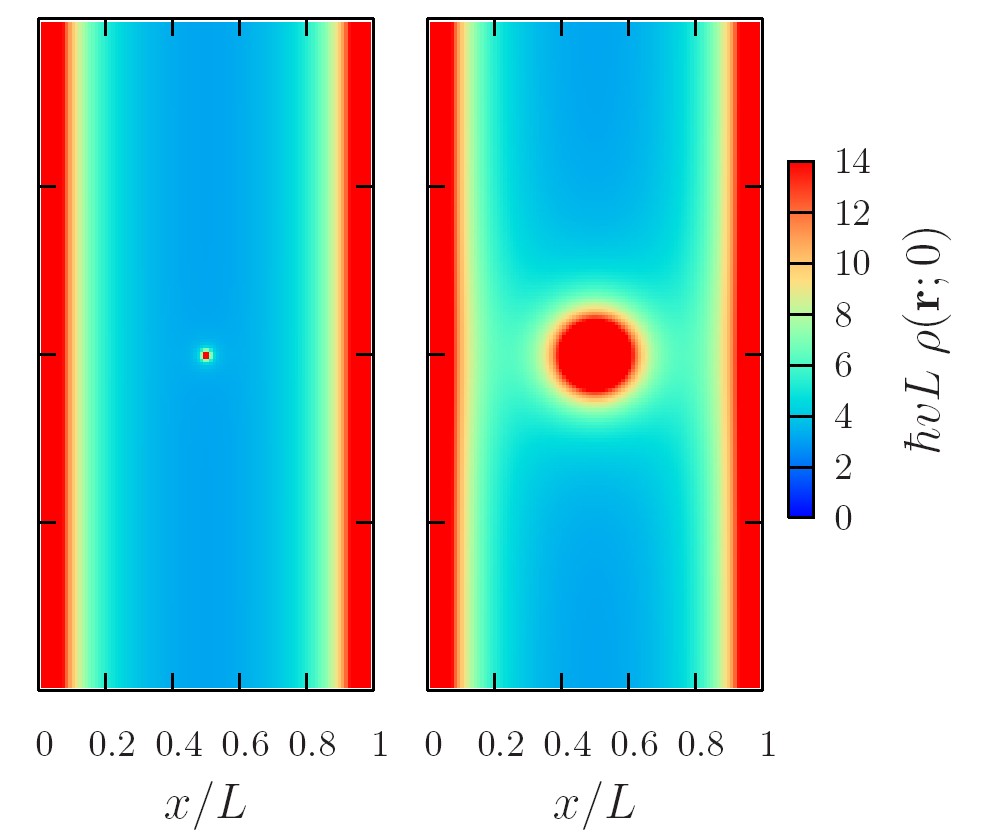
The subproject is intended to develop a comprehensive theoretical picture of electronic transport in graphene structures, involving all the key ingredients of modern nanoscience: namely, quantum interference, quantum criticality, disorder-induced mesoscopic fluctuations, and Coulomb correlations. The emphasis is put on transport properties of disordered two-dimensional graphene-based systems with various kinds of disorder [1]-[5]. We have demonstrated the absence of Anderson localization in graphene for two broad classes of randomness: (i) disorder which respects the chiral symmetry of graphene [1] and (ii) long-range disorder which does not mix the two valleys of graphene spectrum [2]. The conductivity of graphene in the presence of experimentally relevant strong (resonant) impurities and vacancies has been recently analyzed in Refs. [3]-[5]. Another direction of research is focussed on peculiarities of Coulomb interaction and electron-phonon interaction in graphene. The localization and strong correlations in quasi-2D (multi-layers) and quasi-1D systems such as graphene nanoribbons and carbon nanotubes are also studied within the subproject. The objectives of the project are expected to be particularly relevant to the rapidly growing field of nanotechnology, especially in the emergent carbon-based nanoelectronics.
References
|
[1] |
P.M. Ostrovsky, I.V. Gornyi, and A.D. Mirlin, Electron transport in disordered graphene, Physical Review B 74, 235443 (2006) |
|
[2] |
P.M. Ostrovsky, I.V. Gornyi, and A.D. Mirlin, Quantum criticality and minimal conductivity in graphene with long-range disorder, Physical Review Letters 98, 256801 (2007) |
|
[3] |
M. Titov, P.M. Ostrovsky, I.V. Gornyi, A. Schuessler, and A.D. Mirlin, Charge transport in graphene with resonant scatterers, Physical Review Letters 104, 076802 (2010) |
|
[4] |
P. M. Ostrovsky, M. Titov, S. Bera, I. V. Gornyi, and A. D. Mirlin, Diffusion and criticality in undoped graphene with resonant scatterers, Physical Review Letters 105, 266803 (2010) |
|
[5] |
J. Schelter, P. M. Ostrovsky, I. V. Gornyi, B. Trauzettel, and M. Titov, Color-dependent conductance of graphene with adatoms, Physical Review Letters 106, 166806 (2011) |
List of Publications 2006-2011 as PDF
Subproject Report 2006-2010 as PDF