B2.9: Non-Equilibrium Transport through Nanostructures: Electronic Correlations
Subproject Leader: Peter Wölfle
Institut für Theorie der Kondensierten Materie, KIT
Contributing Scientists:
Present: Khandker Muttalib, Alexander Branschädel
Past: Tobias Kuechel, Christine Köhler,
How Quantum Many-Body Effects Influence the Transport of Electrical Charge and Spin in Nano-Structures
The transport of electrons in nanostructures is strongly affected by the Coulomb interaction between electrons. A number of important effects following from there have been experimentally observed over the past two decades, such as the Coulomb blockade, the Kondo effect , Luttinger liquid behaviour, magnetic ordering phenomena, and more. In many cases the electron system is strongly correlated, meaning that complex many-body effects are present. In this project we developed a theoretical description of some of the situations of interest, in particular (1) nanostructures showing the Kondo effect, and (2) quantum transport in disordered ferromagnetic films.
Following a theoretical prediction in the 1980s, the Kondo effect in quantum dots has been observed as a dominant feature in the current-voltage characteristics. A Kondo effect appears whenever a quantum dot with low lying internal degrees of freedom (e.g. a spin) is coupled to reservoirs. Then, at low temperatures a Kondo resonance forms in the local density of states, which allows for resonant tunnelling through the dot and leads to a drastically enhanced conductance, up to the maximum possible.
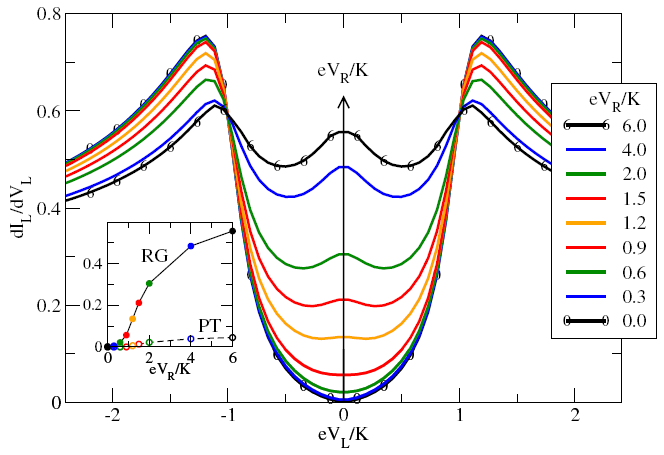
During the last funding period we developed a systematic and controlled method for calculating the conductance of a Kondo dot at bias voltages larger than the characteristic energy of the Kondo effect. Our approach makes use of the perturbative renormalization group method, generalized to out of equilibrium situations. Three new elements have to be added: (1) the renormalized Kondo coupling becomes a function of energy, (2) the renormalization group flow is cut off on the scale of the spin relaxation rate, which is growing large at finite bias, (3) in a magnetic field the spin occupation is non-thermal and is driven by the current through the dot. A finite bias voltage acts to suppress the Kondo resonance, and an external field coupling to the pseudo-spin tends to shift its effect to finite bias. In some cases the Kondo effect is initiated by the finite bias. We have applied our method to a number of systems of more complex structure, with excellent success. A microscopic derivation of our initially semi-phenomenological formulation has been given in the framework of the Functional Renormalization Group method.
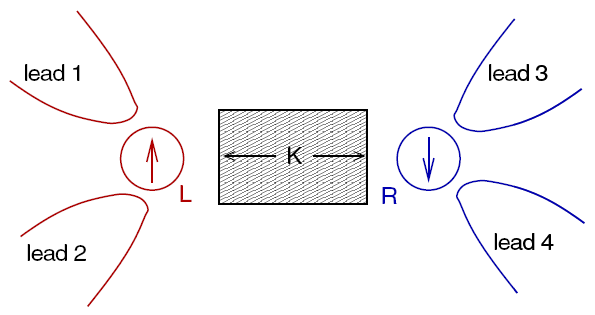
Trans-Conductance of Exchange Coupled Double-Dot System
Consider two quantum dots, each carrying a spin ½, coupled by anti-ferromagnetic spin exchange interaction only (no tunneling or coupling of the charges), each attached to a pair of leads (see Fig. 1). Then the electrical current flowing through dot A will be influenced by the current flowing through dot B. This magical action happens because the transport through either dot depends sensitively on whether the two spins are in their spin singlet (S=0) ground state, or in the spin triplet excited state. The system is in fact a transistor of a new kind (see Fig.2)
Nonequilibrium Singlet-Triplet Kondo Effect in a Carbon Nanotube Quantum Dot
A conducting carbon nano-tube may be contacted to form a quantum dot (Fig. 7). The electronic structure of carbon nano-tubes is characterized by a series of groups of two almost degenerate orbitals, which are both spin doublets. In the standard plot of conductance versus gate voltage and bias voltage, the “Coulomb diamonds” show a corresponding fourfold periodicity. The diamonds assigned to N=1,3 electrons occupying the highest group of levels display a zero bias anomaly signalling the Kondo effect. By contrast, in the case N=0,2 electrons there is no zero bias anomaly. Instead, in the N=2 case, one finds Kondo-like peaks at finite bias V, showing logarithmic growth for decreasing temperature. In a finite magnetic field the peak is found to split into three peaks. This may be understood qualitatively by observing that there are excited states where one electron is promoted from the lower level to the upper level, the two electrons forming a spin S=1 triplet state. That local spin S=1 may undergo a Kondo effect, and it will split into the three sub-states in a magnetic field .
Quantum Transport in Ultrathin Ferromagnetic Films
Quantum corrections to the conductivity of disordered metallic films have been the subject of numerous investigations since the 1980s. One finds two types of corrections, a weak localization correction and an interaction induced (Altshuler-Aronov) correction both increasing logarithmically with decreasing temperature. A very interesting new situation arises in ferromagnetic films due to the presence of spin wave excitations. There films one encounters the so called anomalous Hall effect, i.e. a Hall effect caused by the ferro-magnetically aligned magnetic moments. We have calculated the quantum corrections for this quantity as well and find, among other things that there is no interaction induced quantum correction to the Hall conductivity. Our predictions have been beautifully observed in experiments on Iron and on Gadolinium films with sheet resistances of less than 3 kΩ.
References
|
[1] |
A. Rosch, J. Kroha, J. Paaske, and P. Wölfle, Phys. Rev. Lett. 90, 76804 (2003) |
|
[2] |
H. Schmidt, P. Wölfle, Ann. Phys. (Berlin) 19, 60 (2010) |
|
[3] |
V. Koerting, P. Wölfle, and J. Paaske, Phys. Rev. Lett. 99, 36807 (2007) |
|
[4] |
J. Paaske, A. Rosch, P. Wölfle, N. Mason, C.M. Marcus, and J. Nygard, Nature Physics 2, 460 (2006) |
|
[5] |
P. Mitra, R. Misra, A. F. Hebard, K. A. Muttalib, and P. Wölfle, Phys. Rev. Lett. 99, 46804 (2007) |
List of Publications 2006-2011 as PDF
Subproject Report 2006-2010 as PDF