What is a Topological Insulator?

A band insulator is a crystalline material with the chemical potential lying between the electron bands. At low temperatures the bands are either fully occupied or empty preventing the motion of electrons. In other words, an insulator has no excitations with arbitrary low energies. The situation changes dramatically if the strong spin-orbit interaction comes into play. In the materials composed of heavy elements electron spin strongly interacts with the atomic electric field. In an extreme case this may lead to the spectrum inversion: the bands interchange in energy and the gap between them becomes negative. The topological insulator is an insulator with chemical potential lying inside such an inverted gap. When the topological insulator is contacted with an ordinary insulator, the gap gradually changes from a positive to a negative value and inevitably closes at some point. The physical consequence is the appearance of low energy states localized near the interface. Thus the metallic phase arise in the contact between topological and ordinary insulator.

What is Topological in a Topological Insulator?

Topology is an abstract mathematical theory dealing with very general properties of geometrical objects. These are the properties that cannot be changed by any continuous transformations. How does topology arise and what it tells us about insulators with inverted gap? It tells us that the metallic state we have just described is extremely robust to a broad class of possible perturbations. Appearance of the metallic phase between two kinds of insulators is related to the very general topological fact: any continuous function must pass through zero in order to change its sign. Almost any microscopic modifications in the considered materials are unable to remove the low-lying excitations at their contact. One extreme modification is the complete removal of the normal insulator from the junction. It can be thought of as a continuous increasing of the band gap all the way to infinity. Ultimately, the vacuum (possessing no electronic states whatsoever) is nothing but an extreme case of a usual insulator. This leads us to the conclusion that the metallic state exists just on a free surface of the topological insulator.

Topology Versus Localization

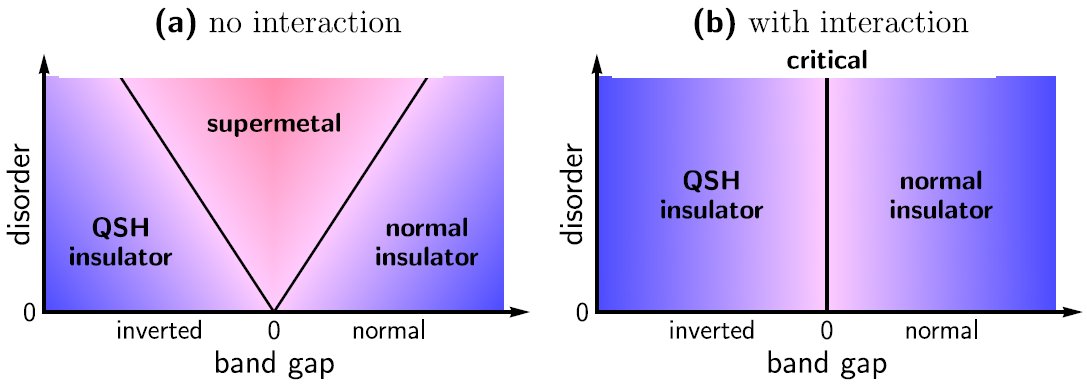
Impurities inevitably present in any materials can have a dramatic effect in usual metals. Even a relatively small random potential may destroy the metallic phase and completely localize electrons due to quantum interference effects: the phenomenon known as Anderson localization. This mechanism however is ineffective in topological insulators: the electrons on their surface are protected by topology and disorder does not localize them. Topological protection of the surface states occurs not only in the materials with strong spin-orbit interaction but also in in systems with other symmetries [1, 2]. In particular, integer quantum Hall effect is an example of the two-dimensional topological insulator with broken time-reversal invariance. Quantization of Hall conductivity is the result of the interplay between topology and localization phenomena. Different topological states of a quantum-Hall topological insulator are separated by quantum phase transitions. Scaling properties of these transition are particularly non-trivial in the presence of interaction [3].

Edge States Interferometry

Edge modes of a quantum Hall sample realize the topologically protected one-dimensional metallic state. Interference of these edge modes was experimentally observed both in integer and fractional quantum Hall regime in the Mach-Zehnder and Fabry-Perot interferometer setup. Coulomb interaction, which is particularly strong in one spatial dimension, leads to strong variations of the visibility of interference pattern with changing the bias voltage [4].

2D Topological Insulator: Quantum Spin-Hall Effect

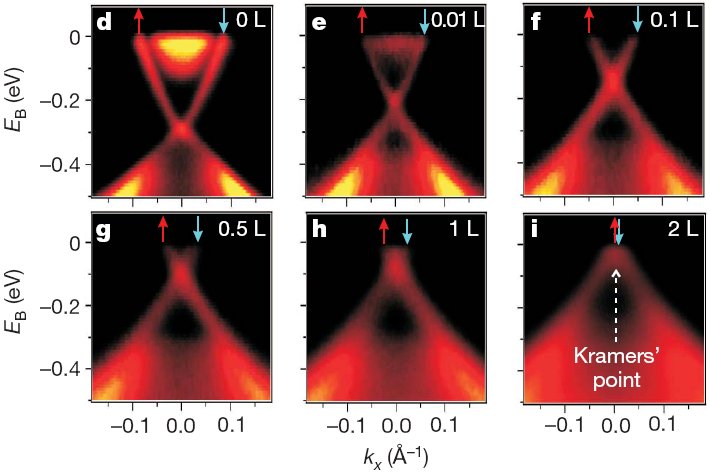
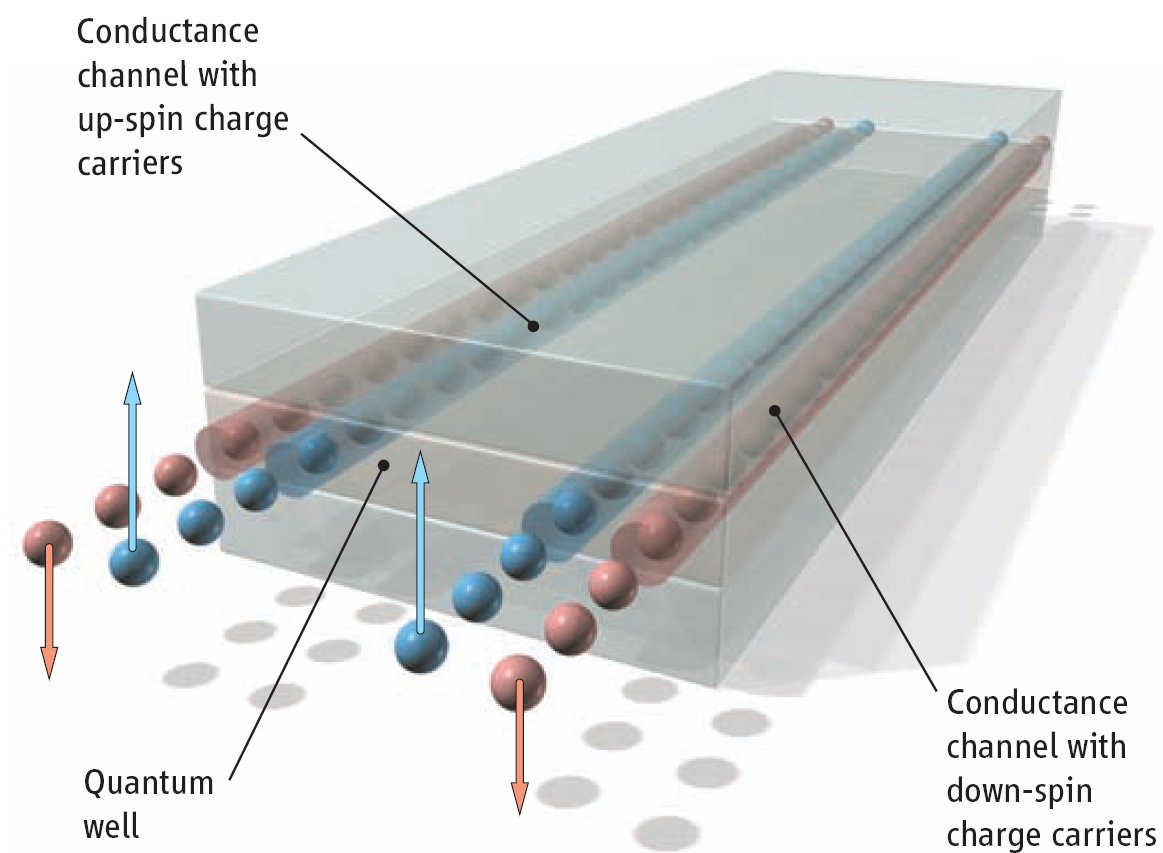
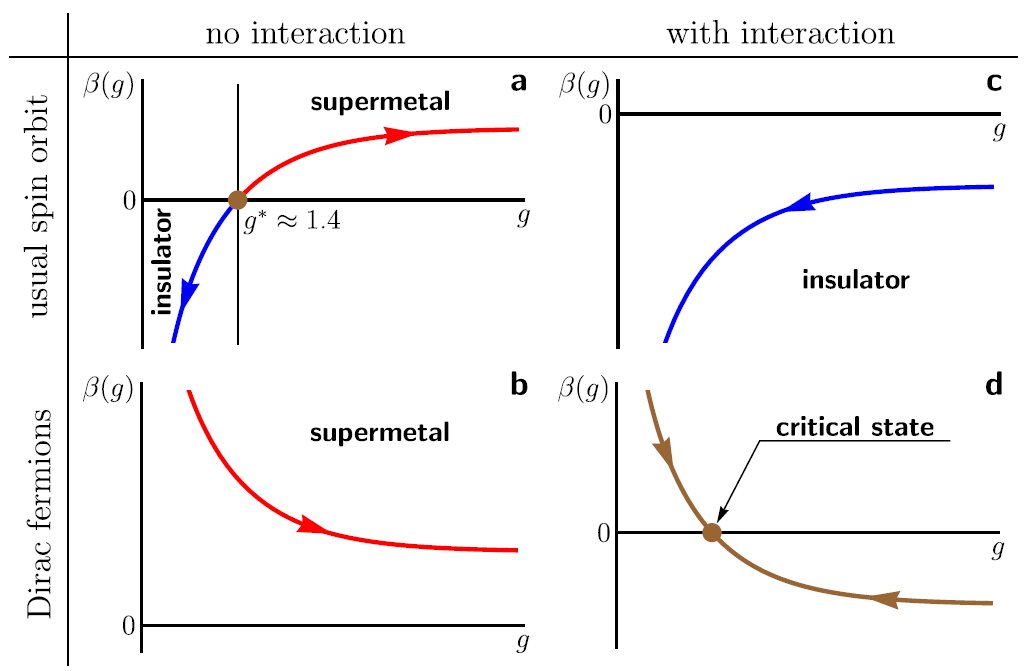
For the first time a topological insulator with preserved time-reversal symmetry (no magnetic field) was implemented by the group of Prof. Molenkamp in the Würzburg University in 2007 [M. König et al., Science 318, 766 (2007)]. The conductance of a thin layer of HgTe was measured with the result very close to 2e2/h. This indicates exactly two perfectly conducting channels in the whole sample. These are the electron channels at the two edges of the sample containing all the low-energy excitations of the system. The perfect conductance of these two one-dimensional “wires” is the direct manifestation of the topological protection. Strong spin-orbit coupling in HgTe leads to spin polarization of the edge channels and hence to the quantum spin-Hall effect: a voltage applied to the sample results in the perpendicular spin current. This phenomenon has a broad range of prospective applications including generation and detection of spin currents as well as conversion between normal and spin current. Interplay of Coulomb interaction and disorder effects leads to the novel quantum critical state occurring at the point of the quantum spin-Hall phase transition [5].

3D Topological Insulator: Topologically Protected Surface States

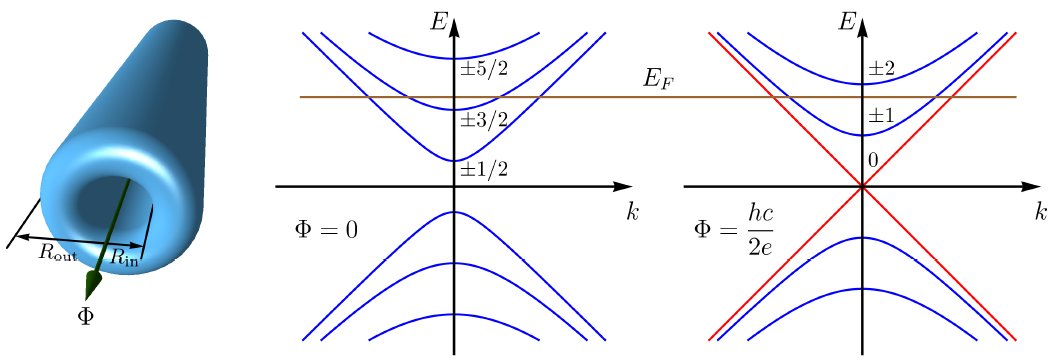
The topologically protected two-dimensional metal occurring on the surface of a three-dimensional topological insulator was first observed at Princeton University in 2008. Low-energy electron excitations were discovered at the surface of the BiSb crystal [M. Z. Hasan and C. L. Kane,Rev. Mod. Phys. 82, 3045 (2010)]. Afterwards similar properties were found in BiSe, BiTe, and some other materials. Electrons on the surface of a topological insulator are described by the massless Dirac Hamiltonian similar to graphene. Analogues of numerous fascinating electronic properties of graphene are thus also expected in topological insulators.   However, one important difference is the lack of valley and spin degeneracy making the surface of a topological insulator just a “quarter” of graphene. This significantly enhances effects of Coulomb interaction in topological insulator and may lead to novel strongly correlated electron phases [5] and even to the emergence of fractional topological insulators.

Topological Superconductors

Topologically protected surface modes may arise not only in an insulator but also in a superconductor possessing a bulk energy gap due to Cooper pairing. Such materials are referred to as topological superconductors. Under certain conditions the surface excitations realize bound Majorana states described by a self-conjugate fermionic field. Majorana states are promising candidates for realizing stable quantum computations and their experimental realization is of a particular importance. First experimental reports on topological superconductors have appeared in 2010 [L. A. Wray et al, Nat. Phys. 6, 855 (2010); J. L. Zhang et al, PNAS 108, 24 (2011)]. Physical properties of these materials and their potential applications are being intensively studied at the moment.

References

List of Publications 2006-2011 as PDF

Subproject Report 2006-2010 as PDF